当有多重递归的时候,人脑无法模拟出递归过程,因此需要借助递归树

#include <iostream>
#include <vector>
using namespace std;
void recursion(vector<int>& nums,vector<int>& temp,int target, int sum,int count,int& len,int current){
//递归三部曲
//- 确定参数和返回值
//- 确定终止条件
//- 单层递归逻辑
if(sum>=target){
//这里只有递归的时候才会调用
len = min(len, count);
return;
}
for(int i=current;i<nums.size();i++){
//原本是4,先回溯到4,for循环结束
//开始第二个回溯,i=3(这个时候sum和count还有temp都减掉了i=3和i=4的情况),经过for之后i=4
// 然后sum加上了i=4的情况,忽略i=3
//之后再回溯到i=2,经过for之后i=3(这里又开始叠加两层递归(i=3和i=4),
//并且对于i=3来说,i=2的值是没有的因为被回溯来,对于i=4来说,这个是i=3的孩子结点)
//通过递归树来分析所有的递归流程
count++;
sum += nums[i];
temp.push_back(nums[i]);
recursion(nums, temp,target,sum,count,len,i+1);
//这里开始回溯,sum和count还有temp都回溯了,但是注意i没有
sum -= nums[i];
temp.pop_back();
count--;
}
}
int minSubArrayLen(int s, vector<int>& nums) {
int len=999;
vector<int> temp;
recursion(nums,temp,s,0,0,len,0);
if (len==999)
return 0;
return len;
}
int main(int argc, const char * argv[]) {
// insert code here...
vector<int> nums={1,2,3,4,5};
int len = minSubArrayLen(15,nums);
cout << len<<endl;
return 0;
}
以下这些都可以用递归回溯来解决
- 组合问题
- 子集问题
- 分割问题
- 排列组合问题
- 棋盘问题
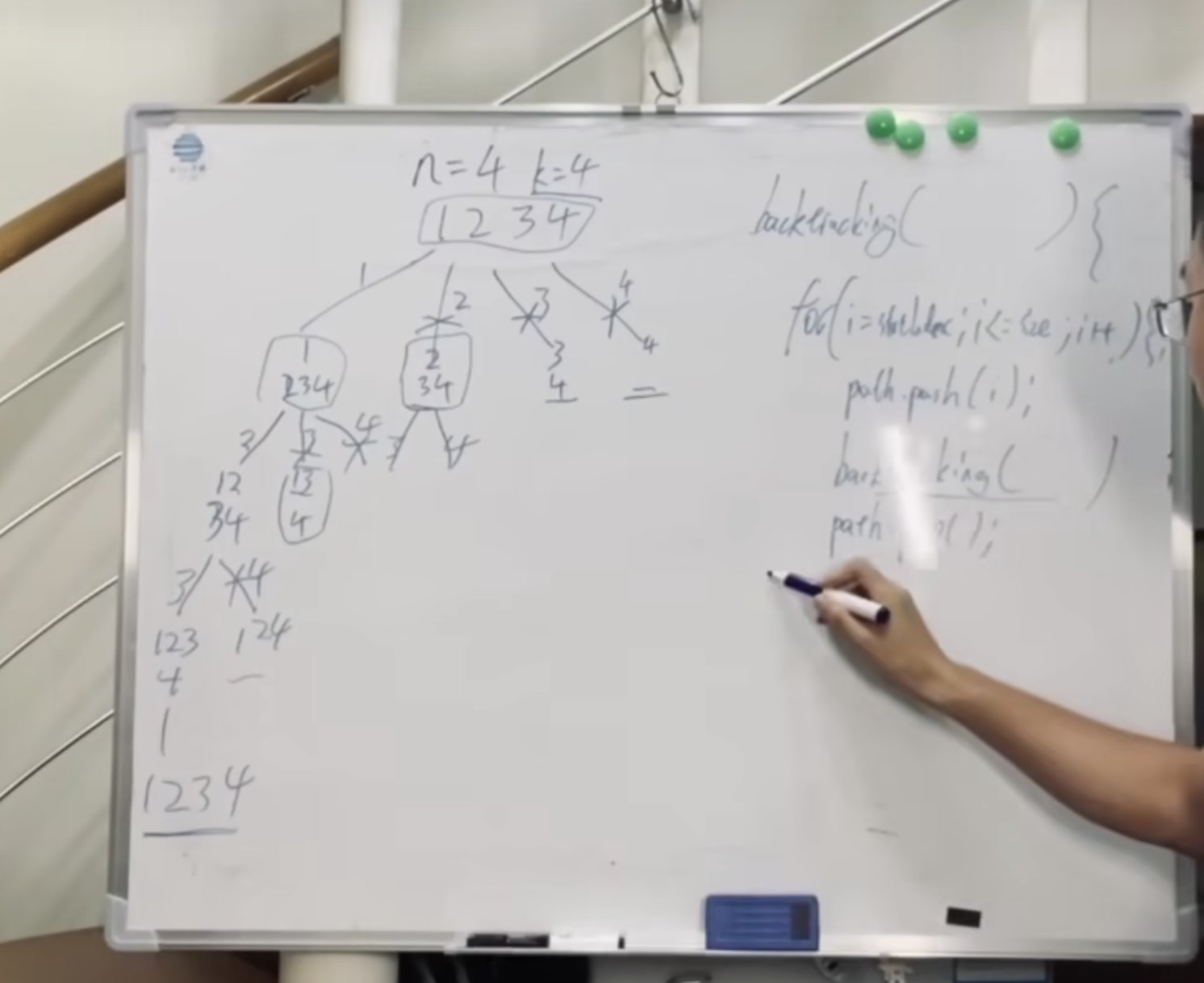
遇到这些问题记得先画递归树



