分治法

分治法：找子解，最后结合子解，比如需要找子解的最小值或最大值作为原问题的解

//
//  main.cpp
//  两个数组调整为一样的最小距离
//
//  Created by moule on 2022/9/3.
//

#include <iostream>
#include <vector>
using namespace std;
int minimal_distance(vector<int>& num1, vector<int>& num2, int idx1, int idx2){
    
    if(idx1 == num1.size() && idx2 == num2.size()){
        return 0;
    }
    if(idx1==num1.size() && idx2 != num2.size()){
       // cout << idx2 << endl;
        int k = num2[idx2] + minimal_distance(num1, num2, idx1, idx2+1);
        return k;
    }
    if(idx2==num2.size() && idx1 != num1.size()){
       // cout << idx2 << endl;
        return num1[idx1] + minimal_distance(num1, num2, idx1+1, idx2);
        
    }
    // delete num1[idx1]
    
    int p1 = num1[idx1] + minimal_distance(num1, num2, idx1+1, idx2);
 //   cout << p1;
    // delete num2[idx2]
    int p2 = num2[idx2] + minimal_distance(num1, num2, idx1, idx2+1);
   // cout << p2;
//    // num1[idx1] - num2[idx2]
    int p3 = abs(num1[idx1]-num2[idx2]) + minimal_distance(num1, num2, idx1+1, idx2+1);
   
    
    return min((p1,p2),p3);
}
int main(int argc, const char * argv[]) {
    // insert code here...
    vector<int> num1 = {2,3};
    vector<int> num2 = {2,3,5};
    cout << minimal_distance(num1, num2, 0, 0) << endl;
    std::cout << "Hello, World!\n";
    return 0;
}

比如汉诺塔问题，汉诺塔问题就是子问题，不需要结合子解，全部的子解就是整个问题的解

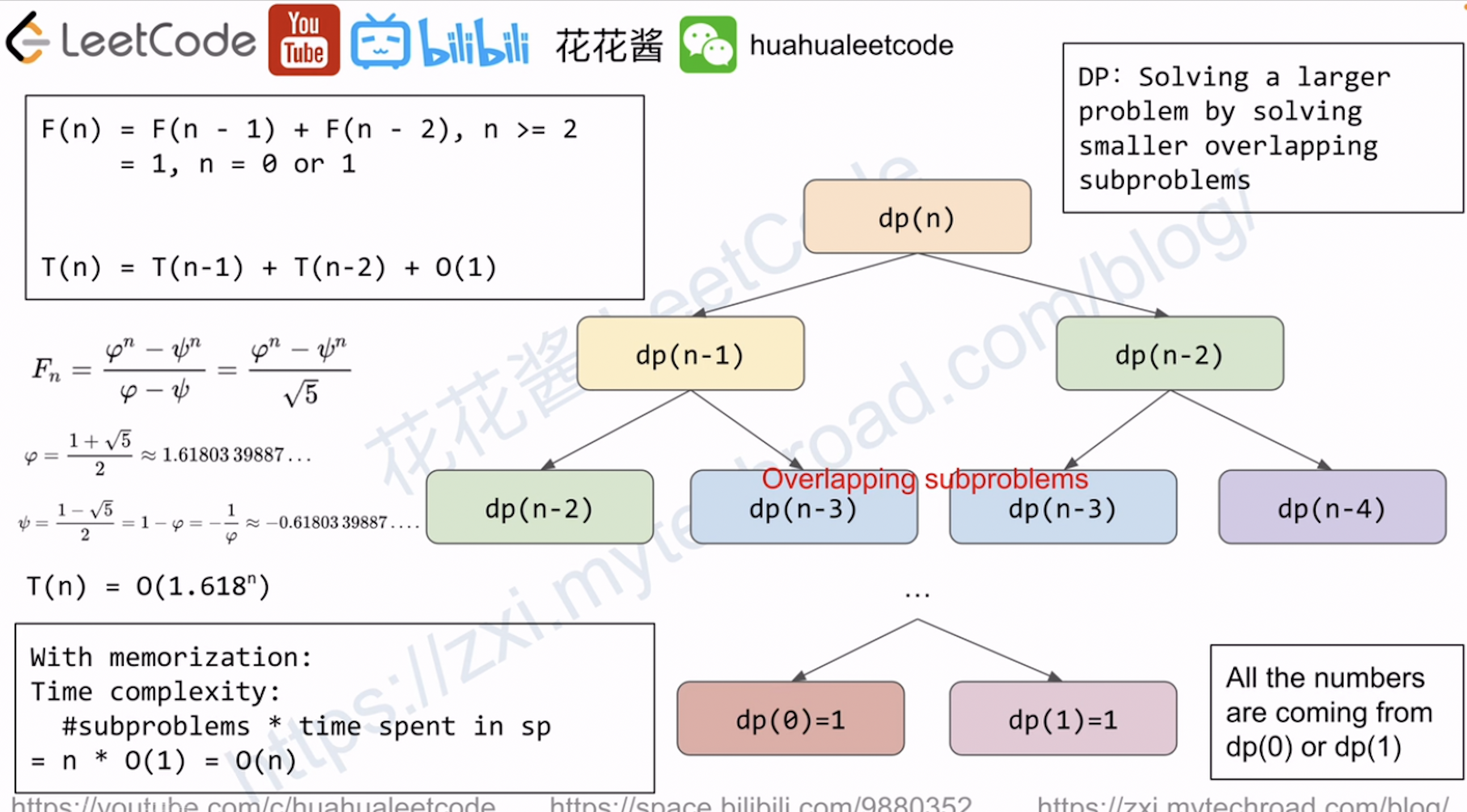
汉诺塔的子问题如下：

- 1）把 N-1个盘子 移到中转柱
- 2）把第N个盘子移动到 目标柱
- 3）把中转柱上面的N-1个盘子借助目前空闲的柱子 移动到 目标柱。

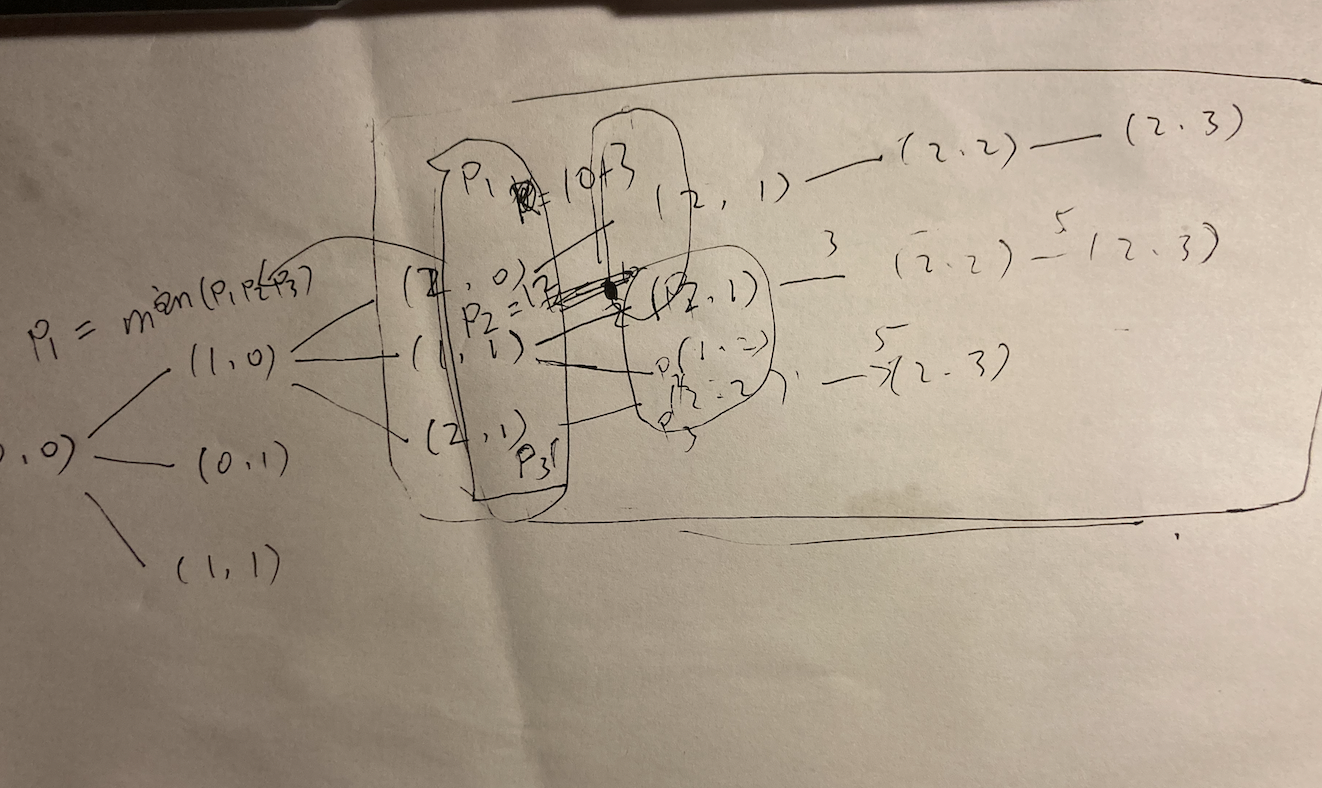
两个数组变为一样的子问题

- 1）第一个数组的下标数删掉
- 2）第二个数组的下标数删掉
- 3）删掉两个数组对应下标数值的差
合：找到三个子解代价最小的